J ohn Horton Conway è sempre stato un predestinato: bambino prodigio, a tre anni recitava le potenze del 2 e a undici, quando a scuola gli chiedevano cosa avrebbe fatto da grande, rispondeva senza esitazioni: “il matematico”. Il curriculum vitae avrebbe poi precisato: matematico per vent’anni a Cambridge e trenta all’Institute of Advanced Studies di Princeton – nella cattedra che fu di John Von Neumann – con contributi importanti in teoria dei numeri, teoria dei giochi, algebra, geometria, topologia, analisi, fisica teorica.
Secondo una famosa definizione del matematico polacco Marc Kac, esistono due tipi di genio: il genio “ordinario” e il “mago”. “Un genio ordinario è un tipo come potrebbe essere uno di noi se solo fosse molte volte più bravo. Non c’è nessun mistero nel modo in cui funziona la sua mente. Con i maghi è diverso. Sono, per usare un’espressione dei matematici, nel complemento ortogonale rispetto a dove stiamo noi, il funzionamento della loro mente ci è del tutto incomprensibile”. Kac coniò la definizione per Richard Feynman, uno dei più famosi e brillanti scienziati del secolo scorso, ma è un gioco che si può generalizzare. E in ambito matematico il nome di Conway viene senza dubbio in mente come possibile mago, tra Alan Turing e Kurt Gödel.
John Conway è morto il mese scorso in New Jersey, per colpa della COVID-19. Ricostruire oggi la sua biografia è come cadere nella tana del Bianconiglio: ogni informazione che si scopre è un mondo nuovo da approfondire, partendo dai suoi risultati su gruppi algebrici giganteschi, passando per la lunga lista di cose che hanno nominato in suo onore, per i giochi da lui inventati, o le amicizie con maghi come lui. Fra queste ultime, spicca quella con Martin Gardner, il giornalista e divulgatore scientifico che contribuì a rendere famoso Conway dalla sua leggendaria rubrica di curiosità matematiche su Scientific American. O quella con Donald Knuth, Grande Mago degli algoritmi, nonché inventore, negli anni Settanta, di TeX, il programma di tipografia digitale diventato subito standard per la stesura di testi scientifici e matematici.
Più di ogni altra cosa al mondo, a Conway piaceva giocare: e giocò, sempre.
Conway attraversò la scuola e l’università con quel misto di indolenza e voti altissimi che promettevano un futuro da scienziato di prima grandezza. Ma la predestinazione può essere una condanna: quando le aspettative sono troppo alte, il fallimento è sempre dietro l’angolo. Il fatto – semplice e capitale – è che, più di ogni altra cosa al mondo, a Conway piaceva giocare: e giocò, sempre. Anche dopo la laurea, negli anni giovanili che per i matematici sono considerati i più importanti e fecondi, Conway amava piazzarsi nella stanza comune dell’università e sfidare gli altri studenti a scacchi, a Go ma soprattutto a giochi di sua invenzione, magari usando frutta secca sulla scacchiera e mangiando via via le pedine dell’avversario.
Arrivò in questo modo fino a trent’anni senza davvero aver prodotto nulla di eccezionale, e la sua frustrazione a riguardo iniziava a diventare opprimente. Poi, nel 1968, su suggerimento di un collega, Conway iniziò a lavorare ad un reticolo algebrico: in pratica, doveva pensare a come riempire un determinato volume con delle sfere: solo che sia il volume che le sfere vivevano in uno spazio a 24 dimensioni, luoghi astratti in cui l’intuizione geometrica è talento di pochissimi. Conway ama ricordare che lavorava seduto su una poltrona, mulinando braccia e gambe, proiettando nella sua mente assi cartesiani aggiuntivi a quelli che siamo in grado di concepire naturalmente e cercando di visualizzare le sue ipersfere.
In poche settimane, con sorpresa, risolse il problema scoprendo un gruppo algebrico composto da ben 8315553613086720000 elementi e che si sarebbe rivelato solo uno dei vari sottoinsiemi di quello che è conosciuto oggi in teoria dei gruppi come Mostro: un gruppo ancora più terrificante, contenente tutte le 8 x 10⁵³ possibili simmetrie di un iperoggetto che vive in uno spazio a 196883 dimensioni. In altre parole: un cubo ha 48 simmetrie, cioè può essere ruotato o riflesso in 48 modi diversi e lo vediamo sempre allo stesso modo; similmente un dodecaedro, che ha dodici facce, possiede 120 simmetrie: il Mostro è l’insieme delle simmetrie di un “solido” a duecentomila dimensioni, con tante simmetrie quante sono le particelle elementari che formano il pianeta Giove.
La scoperta del suo gruppo algebrico – prima ancora dei suoi successivi e fondamentali studi sul Mostro – lo rese istantaneamente celebre nel mondo accademico. Ma, soprattutto, lo liberò: avendo finalmente soddisfatto le aspettative che tutti avevano su di lui, era libero dal peso del senso di colpa che si portava dietro da anni. Fece dunque un voto a sé stesso: non si sarebbe più preoccupato dell’importanza o della serietà di cosa voleva studiare. Avrebbe pensato e fatto tutto quello che voleva, senza avere paura di quello che i colleghi avrebbero potuto reputare inutile (in inglese, to floccinaucinihilipilificate, che rimase la parola preferita di Conway).
Libera di vagare senza redini, la mente di Conway iniziò a mangiarsi la matematica, con quel tocco personale ed eccentrico che, in questo ambito, si può attribuire a pochissimi: il tocco di un artista.
Libera di vagare senza redini, la mente di Conway iniziò a mangiarsi la matematica, con quel tocco personale ed eccentrico che, in questo ambito, si può attribuire a pochissimi: il tocco di un artista, il tocco del mago. Si inventò notazioni matematiche per la teoria dei nodi, per i poliedri, per costruire numeri giganteschi. Scrisse, per gioco, l’articolo di matematica più corto del mondo (Can n²+1 unit equilateral triangles cover an equilateral triangle of side > n, say n + ε? Risposta: n²+2 can.) Trovò un modo più semplice per risolvere il cubo di Rubik, è inventò nuovi giochi di prestigio con le carte.
Assieme al fisico Simon Kochen, elaborò il teorema del Libero Arbitrio per la meccanica quantistica, che afferma che “se gli sperimentatori hanno libero arbitrio, allora ce l’hanno anche le particelle elementari”. Scrisse l’algoritmo Doomsday, per calcolare il giorno della settimana di qualsiasi data passata o futura. Aveva programmato il suo computer perché gli fornisse tre date casuali a cui doveva rispondere in meno di dieci secondi, altrimenti si sarebbe spento. Scoprì collegamenti fra il Mostro e le funzioni modulari ellittiche (chiamandolo “il mostruoso chiaro di luna”), gettando un ponte allora sconosciuto fra algebra, funzioni complesse e, successivamente, la teoria delle stringhe. Quindi fra un un insieme a centinaia di migliaia di dimensioni e, forse, l’universo fisico.
Scoprì anche (o inventò?) i numeri surreali, che comprendono tutti i numeri mai pensati (naturali, razionali, irrazionali, reali, transfiniti), sono sia i più piccoli che i più grandi numeri conosciuti e riuniscono in un unico gesto e un’unica notazione secoli di scoperte in teoria dei numeri (ed è così che incontrai Conway per la prima volta, in una vertigine intellettuale: tra le mille pagine di Gödel, Escher, Bach di Douglas R. Hofstadter – l’agone letterario della mia vita: ci ho messo quattro anni e mezzo a finirlo – si parlava di numeri surreali, che non sono utili quasi a nessuno, ma avrei imparato che con Conway succedeva spesso così: leggevi qualcosa di strano, esoterico e bellissimo e il suo nome prima o poi spuntava fuori).
Proprio per i suoi toni e modi da giullare, coltivati per una vita, è difficile distinguere tra divertissement e scoperte importanti: i suoi teoremi sul Mostro sono stati ottenuti durante una fondamentale sistematizzazione dei gruppi algebrici, e i numeri surreali, a detta di molti, sono una scoperta capitale che deve ancora trovare un’applicazione, come spesso accade in matematica. Paradossalmente, Conway stesso “disprezzava” invece come fosse un mero giochino quello che lo ha definitivamente consacrato al grande pubblico: il gioco della vita.
Il gioco della vita
Game of Life è un gioco “a 0 giocatori” che si gioca da solo, indefinitamente.
Si svolge su una griglia di celle quadrate, come una scacchiera per il go o una pagina di un quaderno a quadretti che si estende all’infinito.
Ogni cella ha quindi 8 celle adiacenti, e ha solo due stati: può essere o viva o morta.
In base al numero di celle adiacenti vive o morte, la nostra cella potrà quindi nascere (se ora è morta), continuare a vivere oppure morire.
Il tempo del gioco è un tempo discreto, cioè ad ogni istante, in base a delle regole prestabilite, le celle si accendono o si spengono, per cui la configurazione delle celle in un dato istante viene usata per calcolare lo stato delle celle all’istante successivo.
Le regole sono:
- Qualsiasi cella viva con meno di due celle vive adiacenti muore per isolamento;
- Qualsiasi cella viva con due o tre celle vive adiacenti sopravvive;
- Qualsiasi cella viva con più di tre celle vive adiacenti muore per sovrappopolazione;
- Qualsiasi cella morta con esattamente tre celle vive adiacenti diventa una cella viva, per riproduzione.
Con sole queste quattro regole, Conway creò un piccolo universo in cui strani microorganismi virtuali possono nascere e morire nel giro di qualche secondo, oppure andare avanti all’infinito. Partendo quindi da un disegno iniziale – un numero di celle vive – queste evolveranno in qualcos’altro. Alcune di queste forme rimangono semplicemente in vita, staticamente:
mentre altri, detti oscillatori, ciclicamente ripercorrono lo stesso pattern, in diversi periodi. Possono essere molto semplici, come il blinker, composto da tre celle, che ha periodo 2:
o più complessi e numerosi, come il pulsar, che ha periodo 3:
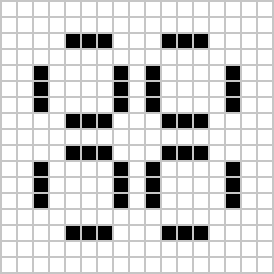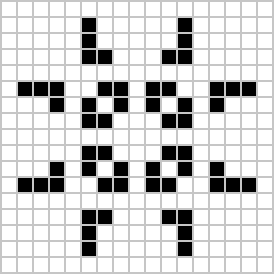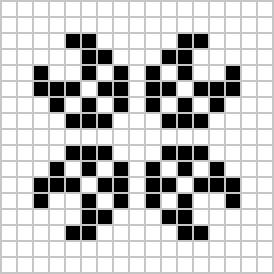
Uno dei più famosi – diventato anche il simbolo internazionale degli hacker – è il glider, che ha la facoltà di spostarsi in diagonale, dirigendosi all’infinito verso le estremità del gioco:
Bill Gosper, nel 1970, scoprì il primo “organismo” a crescita infinita: la sua glider gun poteva creare dei glider in pochi cicli, che poi si allontanavano facendo spazio agli altri.
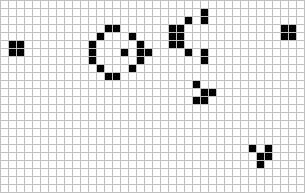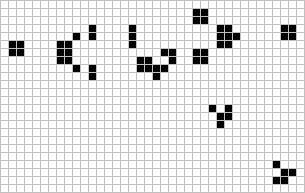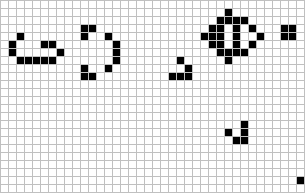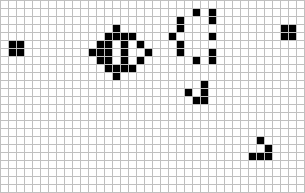
Da allora migliaia di nuove forme sono state scoperte, catalogate e studiate. Tramite l’interazione di queste forme – soprattutto quelle capaci di spostarsi – è possibile costruire dei contatori, ma anche riprodurre elementi logici tipo AND, OR e NOT, che sono la base della logica e quindi dell’informatica. Attraverso costruzioni sempre più ardite e complesse, come il metapixel,
è possibile controllare una singola metacella, costruita con 64691 celle, e farlo accendere o spegnere secondo delle istruzioni, in “sole” 35,328 generazioni.
È stato dimostrato che il gioco della vita è equivalente ad una macchina di Turing: matematicamente, cioè, è un vero e proprio computer. Un’intelligenza gigantesca ed estremamente paziente potrebbe, cioè, trovare la configurazione giusta per far qualsiasi tipo di calcolo dentro il gioco, e simulare ogni tipo di software. In linea puramente teorica, il gioco della vita potrebbe fare qualsiasi calcolo, riprodurre qualsiasi codice: ricreare Facebook, il world wide web, un video di Youtube, essere usato per scrivere un articolo su Google Doc come sto facendo ora. Alcuni ricercatori, qualche anno fa, sono riusciti nella meravigliosa e completamente inutile impresa di implementare Tetris.
Come ricordava sul Tascabile Roberto Paura, con Game of Life Conway è riuscito a dimostrare che anche partendo da regole semplici si può arrivare ad una grande, gigantesca complessità: idea che dagli anni Settanta in poi ha dato grande impulso alle scienze dei sistemi complessi, allo studio degli automi cellulari, dei frattali, del caos.
Uno dei più ambiziosi e ardenti sacerdoti della computazione, Stephen Wolfram – fisico e programmatore, inventore del software Mathematica, milionario, e altro genio – ha recentemente proposto un progetto collaborativo (che è stato anche molto criticato) per costruire una “Teoria del Tutto” che parta da semplici grafi e arrivi a produrre le leggi fisiche, secondo un nuovo paradigma scientifico che sia discreto e non continuo, basato su costruzioni simili ad automi cellulari e non sulle equazioni care ai fisici e ai matematici. Secondo Wolfram l’universo è, fondamentalmente, un computer – quantistico – che calcola sé stesso: idea che gira da decenni fra i fisici e che è la base teorica della recente serie Devs. Gli studi di John Von Neumann prima, e l’invenzione di Conway dopo, sono stati i primi passi verso questo nuovo paradigma.
Game of Life era semplice e geniale, accessibile a chiunque, vertiginoso nelle implicazioni scientifiche e filosofiche. Fatto girare su un computer, ancora oggi dopo 50 anni riesce a sbalordire e affascinare, e proprio per questo, e con suo grande disappunto, Game of Life è diventato in assoluto il risultato più conosciuto di Conway, con milioni di appassionati nel mondo e una vasta letteratura accademica che ne esplora regole, varianti e le diverse forme di vita.
Cosa resta di un mago
Conway fu anche un insegnante straordinario: la sua infantile e inesauribile passione per i giochi gli faceva amare la compagnia degli studenti, che non vedevano l’ora di confrontarsi e sfidare un matematico affermato. Gli aneddoti a riguardo non si contano: praticamente ogni matricola di Cambridge e Princeton ha perso almeno una volta ad uno dei suoi innumerevoli giochi (tanto che spesso, per dare un po’ di vantaggio, permetteva allo sfidante di scambiarsi di ruolo quando se la stava vedendo troppo brutta – e riusciva a vincere comunque). Da professore, durante una lezione sulla simmetria e i solidi platonici, iniziò a intagliare un icosaedro in una grande rapa, con le sue 20 facce triangolari, mangiando via via i pezzi e continuando a spiegare.
L’opera – verrebbe da dire, la poetica – di Conway è la reificazione del fatto, troppo spesso dimenticato nella didattica e nell’insegnamento della matematica, che è possibile creare universi in un foglio di carta, che esiste un entusiasmo, una pura gioia nel giocare matematicamente con il pensiero. Una vertigine che è l’esatto inverso della noia che tutti noi abbiamo provato nell’applicare regole che non capivamo a numeri e lettere che ci parevano inutili.
Ciò che rendeva Conway diverso dagli altri matematici era una curiosità sconfinata: saper trovare interessante anche il gioco per bambini più banale. Come disse James Propp, professore dell’università del Massachusetts : “Conway è quel raro tipo di matematico con una tale abilità di connettere i suoi interessi matematici che ti fa chiedere se per caso non sia capace di modificare la stessa realtà, e non solo esplorarla”. “Conway, con la forza della sua personalità e della sua passione, ha piegato l’universo matematico alla sua volontà”.
L’opera – verrebbe da dire, la poetica – di Conway è la reificazione del fatto, troppo spesso dimenticato nella didattica e nell’insegnamento della matematica, che è possibile creare universi in un foglio di carta.
In matematica, il dibattito tra chi parla di scoperte, piuttosto che creazioni, è ancora aperto: molti matematici, Conway incluso, sono platonici, per cui la matematica è un universo di universi che esiste già, fuori di noi, in un qualche iperuranio.
Tutti questi universi hanno delle loro logiche, e gli oggetti, i numeri, le strutture sono lì, solo che non si vedono. Albergano in dimensioni a noi inaccessibili, come Cthulhu e i mostri di Lovecraft. La matematica è l’unica sonda, l’unica tecnologia che possiamo usare per vederli.
A volte grandi esploratori possono scoprire oggetti che apparentemente, e per decenni o secoli, apparentemente non hanno senso, solo perché loro sono andati molto più avanti degli altri e il sentiero per vedere bene tutto il paesaggio non era ancora stato aperto. Come imbattersi, nella giungla, in un tempio di una civiltà sconosciuta, e ci sei arrivato da solo.
Nelle ultime interviste che si trovano su Youtube, Conway è anziano: ha ottant’anni, ha avuto tre mogli e sette figli, una vita da giullare matematico ma anche piena di dolori, fra cui un tentativo di suicidio di cui parlava anche a lezione (se lo sanno comunque tutti, perché evitare l’argomento?). Eppure è sempre lucidissimo, con un sorriso furbo e spettinato, perennemente in t-shirt come una vecchia rockstar, e si rammarica che i pochi anni che gli rimangono da vivere non gli permetteranno di assistere alla vera comprensione del Mostro: perché esiste, a cosa serve, quali sono i legami profondi che lo rendono un oggetto con un senso all’interno della matematica. Cose che sapremo, forse, solo fra qualche decennio.
L’eredità matematica di John Horton Conway è incalcolabile, anche nei suoi rivoli più minuti. È stato insieme un matematico, un professore, uno showman e un giocatore ad altissimi livelli: un mago. Mi piace pensare che la vera eredità che lascia a noi poveri mortali è la certezza che la matematica è un gioco. E i giochi vanno sempre presi seriamente.
All’inizio era il vuoto, e J.H.W.H. Conway iniziò a creare numeri.
Donald Knuth
La modestia è il mio unico vizio. Non fossi così modesto, sarei perfetto.
John H. Conway
I più letti del mese
